～加斯东's blog～
0%

从零开始写个简单的解释器（8）

发表于 更新于 Disqus：
本文字数： 3.2k 阅读时长 ≈ 3 分钟

原文：Let’s Build A Simple Interpreter. Part 8

译文：

引言与目标

今天我们将讨论一元运算符，即一元加（+）和一元减（-）运算符。

今天的很多内容都基于前一篇文章的内容，因此如果你需要复习，可以回到第七部分重温一下。记住：反复练习是学习的关键。

今天我们将完成以下任务：

  • 扩展语法以处理一元加和一元减运算符
  • 添加一个新的 UnaryOp 抽象语法树（AST）节点类
  • 扩展解析器以生成包含 UnaryOp 节点的AST
  • 扩展解释器，添加新的 visit_UnaryOp 方法来解释一元运算符 让我们开始吧！

目前为止，我们只处理了二元运算符（+、-、*、/），这些运算符作用于两个操作数。

一元运算符

那么什么是一元运算符？一元运算符是只作用于一个操作数的运算符。

以下是关于一元加和一元减运算符的规则：

  • 一元减号（-）运算符对其操作数取反
  • 一元加号（+）运算符不改变其操作数
  • 一元运算符的优先级高于二元运算符 +、-、* 和 /

在表达式“+ - 3”中，第一个‘+’表示一元加运算，第二个‘-’表示一元减运算。表达式“+ - 3”相当于“+ (- (3))”，结果等于**-3**。你也可以说表达式中的-3是一个负整数，但在这里我们将其视为一元减运算符，操作数为正整数3。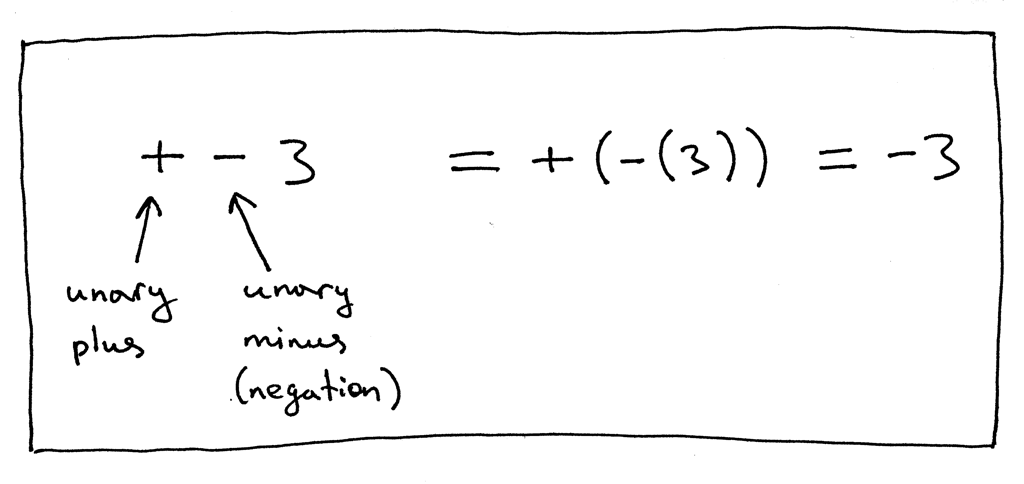

让我们看看另一个表达式，“5 - - 2”：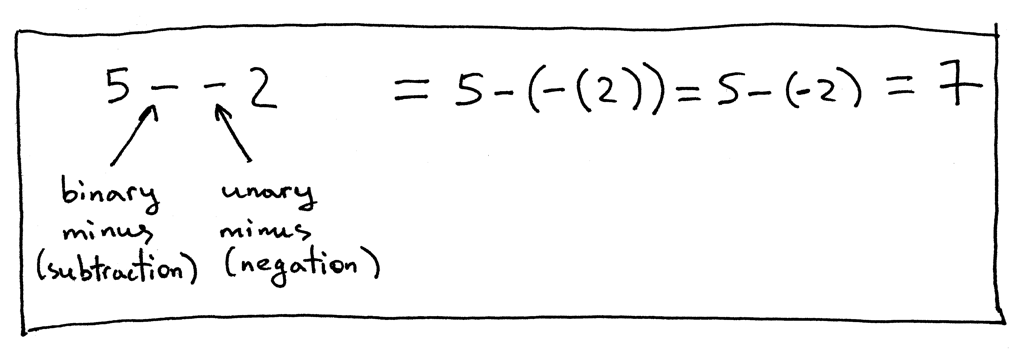

在表达式“5 - - 2”中，第一个‘-’表示二元减法运算，而第二个‘-’表示一元减运算，即取反。

再来看几个例子：


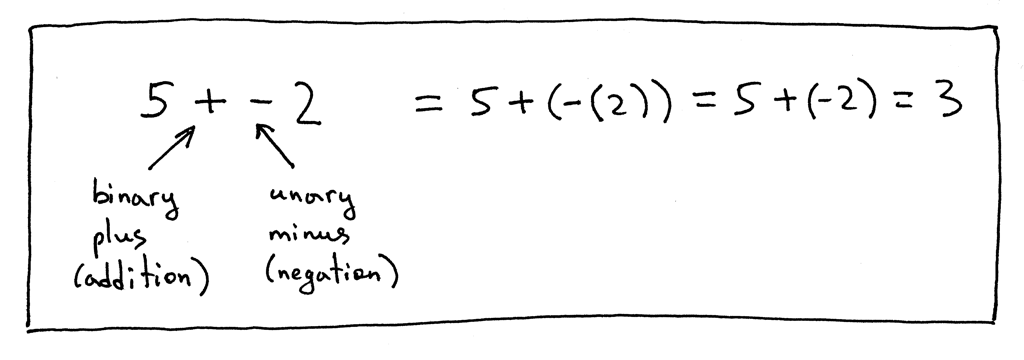
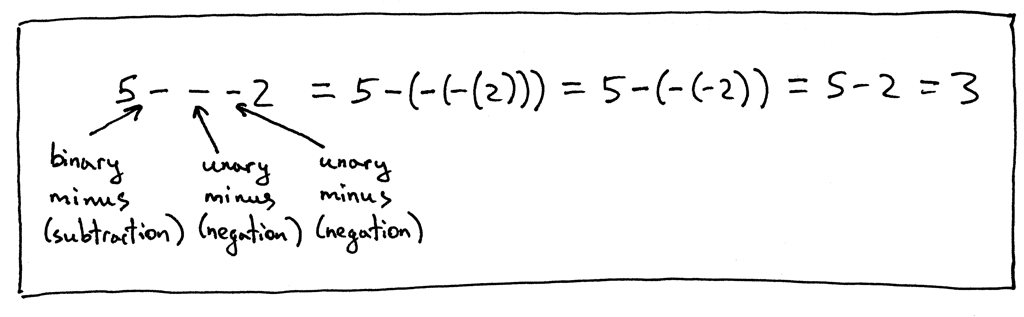
现在我们需要更新语法，以支持一元加和一元减运算符。我们将修改 factor 规则并添加一元运算符，因为一元运算符的优先级高于二元运算符 +、-、* 和 /。

这是当前的 factor 规则：

这是更新后的 factor 规则，以处理一元加和一元减运算符：

如你所见，我扩展了 factor 规则，使其能够自引用，从而可以推导出类似“- - - + - 3”这样的合法表达式，表达式中包含了多个一元运算符。

以下是完整的语法，现在它可以推导出包含一元加和一元减运算符的表达式：

实现与代码解析

下一步，我们将添加一个AST节点类来表示一元运算符。

实现代码如下：

1
2
3
4
class UnaryOp(AST):
    def __init__(self, op, expr):
        self.token = self.op = op
        self.expr = expr

构造函数接受两个参数：op 表示一元运算符的token（加号或减号），expr 表示一个AST节点。

更新后的语法修改了 factor 规则，因此我们也需要在解析器中的 factor 方法中进行相应的调整。我们将在该方法中添加代码以处理 “(PLUS | MINUS) factor” 子规则：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def factor(self):
    """factor : (PLUS | MINUS) factor | INTEGER | LPAREN expr RPAREN"""
    token = self.current_token
    if token.type == PLUS:
        self.eat(PLUS)
        node = UnaryOp(token, self.factor())
        return node
    elif token.type == MINUS:
        self.eat(MINUS)
        node = UnaryOp(token, self.factor())
        return node
    elif token.type == INTEGER:
        self.eat(INTEGER)
        return Num(token)
    elif token.type == LPAREN:
        self.eat(LPAREN)
        node = self.expr()
        self.eat(RPAREN)
        return node

现在我们需要扩展 Interpreter 类，添加 visit_UnaryOp 方法来解释一元节点：

1
2
3
4
5
6
def visit_UnaryOp(self, node):
    op = node.op.type
    if op == PLUS:
        return +self.visit(node.expr)
    elif op == MINUS:
        return -self.visit(node.expr)

继续前进！

接下来，我们手动构建表达式“5 - - - 2”的AST，并将其传递给解释器，以验证新的 visit_UnaryOp 方法是否正常工作。你可以在Python shell中执行以下操作：

1
2
3
4
5
6
7
8
9
10
11
12
13
>>> from spi import BinOp, UnaryOp, Num, MINUS, INTEGER, Token
>>> five_tok = Token(INTEGER, 5)
>>> two_tok = Token(INTEGER, 2)
>>> minus_tok = Token(MINUS, '-')
>>> expr_node = BinOp(
...     Num(five_tok),
...     minus_tok,
...     UnaryOp(minus_token, UnaryOp(minus_token, Num(two_tok)))
... )
>>> from spi import Interpreter
>>> inter = Interpreter(None)
>>> inter.visit(expr_node)
3

从视觉上来看，上述AST的结构如下：

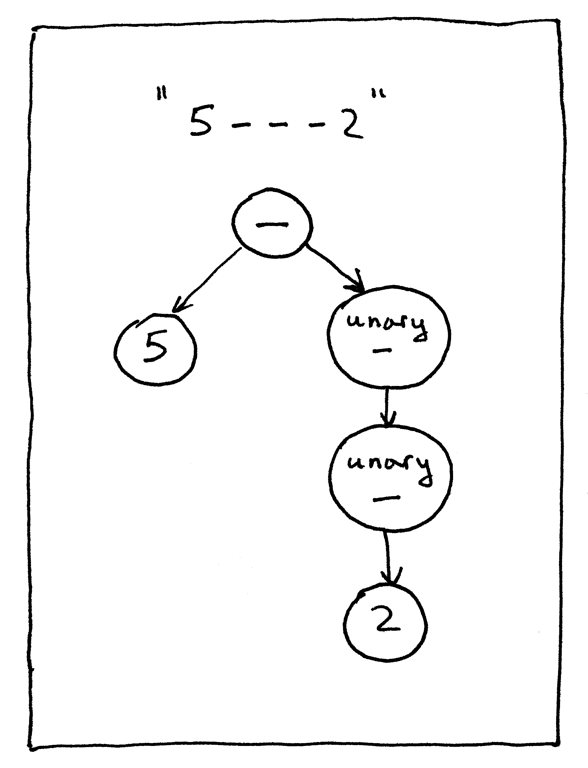
你可以从GitHub直接下载本文解释器的完整源代码。试试看，看看你更新后的基于树的解释器是否能够正确地求解包含一元运算符的算术表达式。

实践与扩展

这是一个示例会话：

1
2
3
4
5
6
7
8
9
$ python spi.py
spi> - 3
-3
spi> + 3
3
spi> 5 - - - + - 3
8
spi> 5 - - - + - (3 + 4) - +2
10

我还更新了 genastdot.py 工具，以支持一元运算符。以下是几个带有一元运算符的表达式生成的AST图像示例：

1
$ python genastdot.py "- 3" > ast.dot && dot -Tpng -o ast.png ast.dot

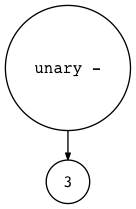
1
$ python genastdot.py "+ 3" > ast.dot && dot -Tpng -o ast.png ast.dot

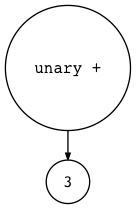
1
$ python genastdot.py "5 - - - + - 3" > ast.dot && dot -Tpng -o ast.png ast.dot

1
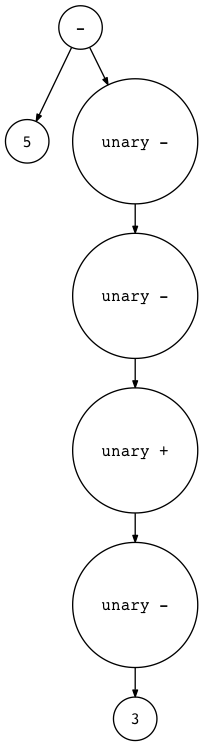
2
$ python genastdot.py "5 - - - + - (3 + 4) - +2" \
  > ast.dot && dot -Tpng -o ast.png ast.dot


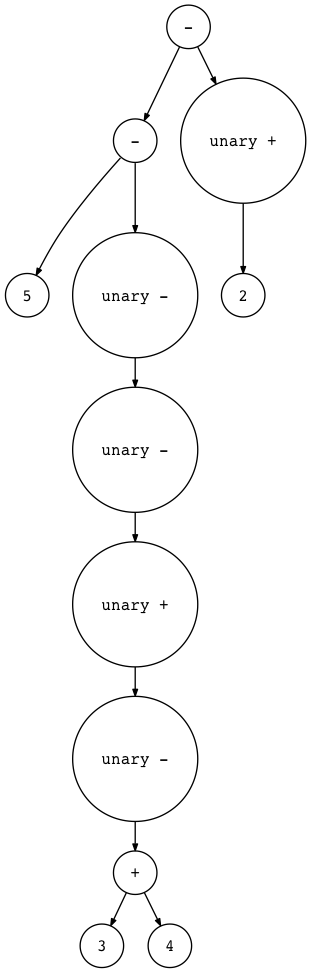
现在来个新练习：

安装 Free Pascal，编译并运行 testunary.pas，验证其结果与 spi 解释器的结果是否一致。

今天的内容到此为止。在下一篇文章中，我们将讨论赋值语句。敬请期待，我们下次再见！

推荐阅读书目列表

以下是我推荐的几本书，它们将帮助你学习解释器和编译器：