～加斯东's blog～
0%

从零开始写个简单的解释器（6）

发表于 更新于 Disqus：
本文字数： 5.7k 阅读时长 ≈ 5 分钟

原文：Let’s Build A Simple Interpreter. Part 6.

译文：

前言

今天是个重要的日子 :) 你可能会问：“为什么？” 因为今天我们将几乎完成对算术表达式的讨论，新增了括号表达式的支持，并且实现了一个能够解析任意深度嵌套括号表达式的解释器。比如表达式 7 + 3 * (10 / (12 / (3 + 1) - 1))。

更新语法

首先，我们需要修改语法以支持括号内的表达式。如你所记得的第五部分，factor 规则用于表达式中的基本单元。在那篇文章中，唯一的基本单元是整数。今天我们要添加另一种基本单元——括号表达式。

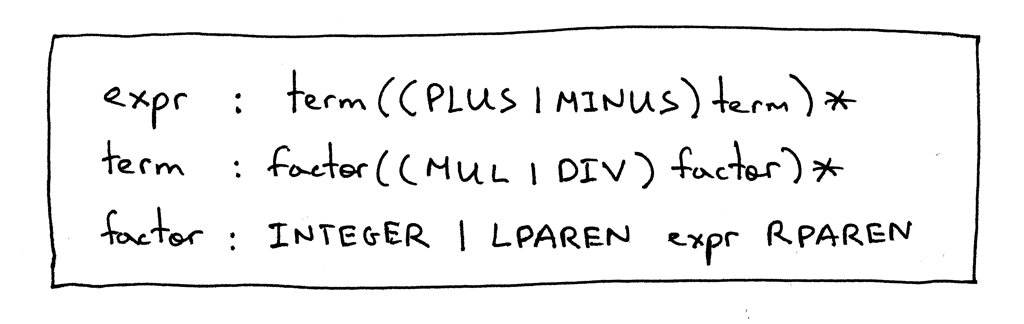
以下是我们更新后的语法：

expr 和 term 的生成规则与第五部分完全相同，唯一的变化是 factor 生成规则，LPAREN 表示左括号 '('，RPAREN 表示右括号 ')'，括号中的非终结符 expr 指代 expr 规则。

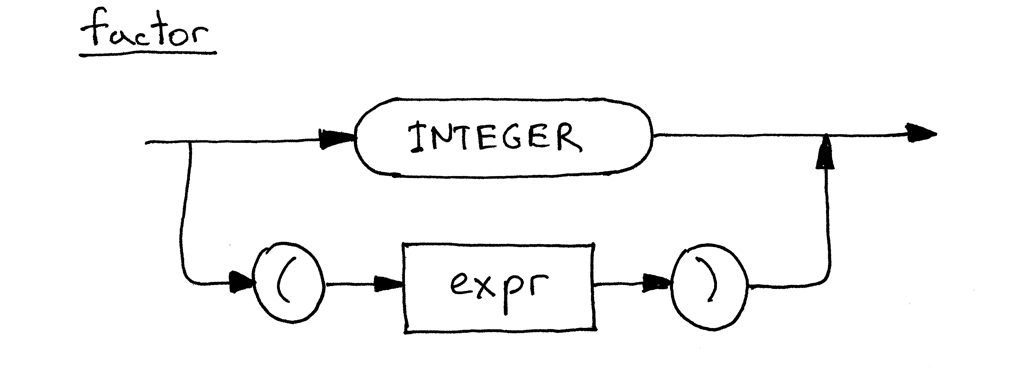
这是更新后的 factor 语法图，现在它包含了多个选项：

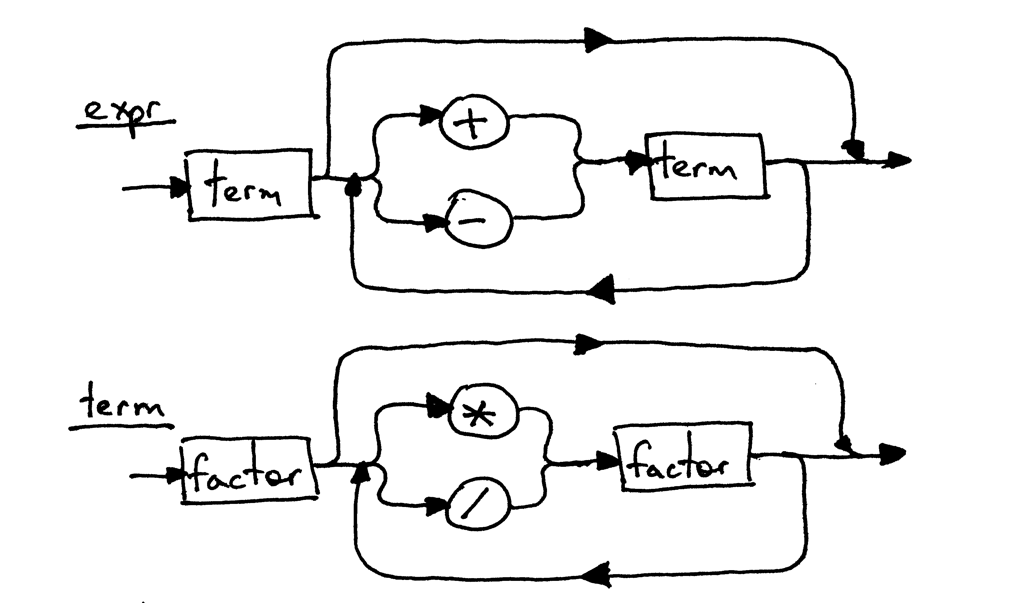
由于 expr 和 term 的语法规则没有变化，它们的语法图与第五部分保持一致：

我们的新语法有一个有趣的特性——它是递归的。如果你推导表达式 2 * (7 + 3)，你将从 expr 开始符号开始，并最终递归地使用 expr 规则推导出 (7 + 3) 部分。

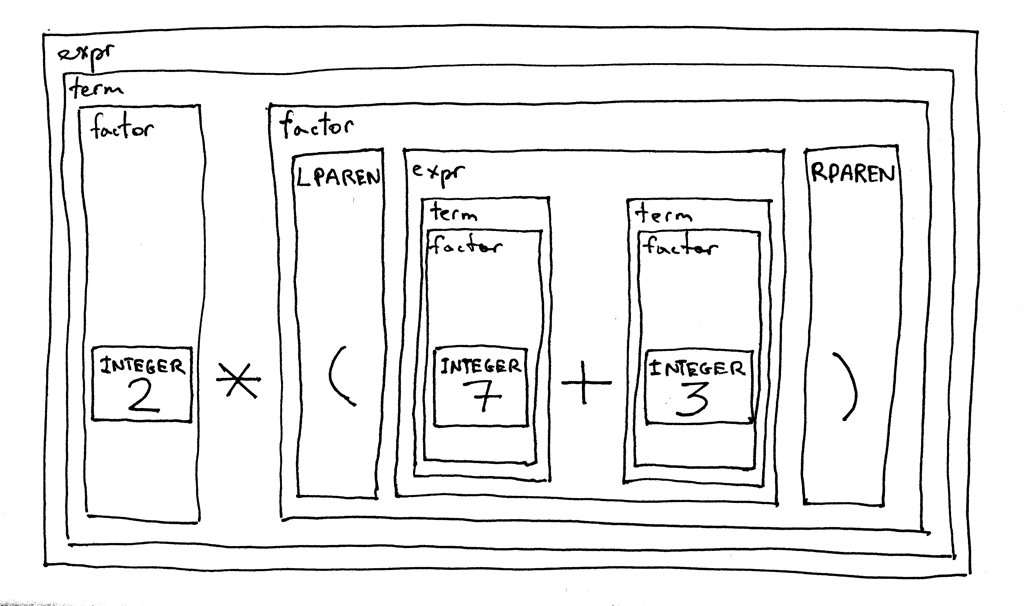
让我们根据语法分解表达式 2 * (7 + 3)，看看它的结构：

如果你需要复习递归知识，可以参考 Daniel P. Friedman 和 Matthias Felleisen 的《The Little Schemer》一书，这本书非常不错。

实现代码

接下来，让我们将更新后的语法转换为代码。

以下是对前一篇文章中的代码的主要修改：

  • Lexer 类新增了两个 token：LPAREN 表示左括号，RPAREN 表示右括号。
  • Interpreter 类的 factor 方法更新，支持解析括号表达式和整数。

以下是一个完整的计算器代码，它可以解析包含整数、任意数量的加减乘除运算符，以及任意深度嵌套括号表达式的算术表达式：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
# Token 类型
#
# EOF（文件结束）token 表示词法分析时没有更多输入
INTEGER, PLUS, MINUS, MUL, DIV, LPAREN, RPAREN, EOF = (
    'INTEGER', 'PLUS', 'MINUS', 'MUL', 'DIV', '(', ')', 'EOF'
)


class Token(object):
    def __init__(self, type, value):
        self.type = type
        self.value = value

    def __str__(self):
        """类实例的字符串表示。

        示例:
            Token(INTEGER, 3)
            Token(PLUS, '+')
            Token(MUL, '*')
        """
        return 'Token({type}, {value})'.format(
            type=self.type,
            value=repr(self.value)
        )

    def __repr__(self):
        return self.__str__()

class Lexer(object):
    def __init__(self, text):
        # 输入的字符串，例如 "4 + 2 * 3 - 6 / 2"
        self.text = text
        # self.pos 是 self.text 的索引
        self.pos = 0
        self.current_char = self.text[self.pos]

    def error(self):
        raise Exception('无效字符')

    def advance(self):
        """前进 `pos` 指针并设置 `current_char` 变量。"""
        self.pos += 1
        if self.pos > len(self.text) - 1:
            self.current_char = None  # 表示输入结束
        else:
            self.current_char = self.text[self.pos]

    def skip_whitespace(self):
        while self.current_char is not None and self.current_char.isspace():
            self.advance()

    def integer(self):
        """返回从输入中提取的多位整数。"""
        result = ''
        while self.current_char is not None and她self.current_char.isdigit():
            result += self.current_char
            self.advance()
        return int(result)

    def get_next_token(self):
        """词法分析器（也称为扫描器或标记器）

        该方法负责将句子分解为 token，每次一个。
        """
        while self.current_char is not None:

            if self.current_char.isspace():
                self.skip_whitespace()
                continue

            if self.current_char.isdigit():
                return Token(INTEGER, self.integer())

            if self.current_char == '+':
                self.advance()
                return Token(PLUS, '+')

            if self.current_char == '-':
                self.advance()
                return Token(MINUS, '-')

            if self.current_char == '*':
                self.advance()
                return Token(MUL, '*')

            if self.current_char == '/':
                self.advance()
                return Token(DIV, '/')

            if self.current_char == '(':
                self.advance()
                return Token(LPAREN, '(')

            if self.current_char == ')':
                self.advance()
                return Token(RPAREN, ')')

            self.error()

        return Token(EOF, None)

class Interpreter(object):
    def __init__(self, lexer):
        self.lexer = lexer
        # 设置当前 token 为从输入中获取的第一个 token
        self.current_token = self.lexer.get_next_token()

    def error(self):
        raise Exception('语法错误')

    def eat(self, token_type):
        # 将当前 token 类型与传入的 token 类型比较
        # 如果匹配，则“吃掉”当前 token，并将下一个 token 赋值给 self.current_token
        # 否则抛出异常。
        if self.current_token.type == token_type:
            self.current_token = self.lexer.get_next_token()
        else:
            self.error()

    def factor(self):
        """factor : INTEGER | LPAREN expr RPAREN"""
        token = self.current_token
        if token.type == INTEGER:
            self.eat(INTEGER)
            return token.value
        elif token.type == LPAREN:
            self.eat(LPAREN)
            result = self.expr()
            self.eat(RPAREN)
            return result

    def term(self):
        """term : factor ((MUL | DIV) factor)*"""
        result = self.factor()

        while self.current_token.type in (MUL, DIV):
            token = self.current_token
            if token.type == MUL:
                self.eat(MUL)
                result *= self.factor()
            elif token.type == DIV:
                self.eat(DIV)
                result /= self.factor()

        return result

    def expr(self):
        """算术表达式解析器 / 解释器。

        calc> 7 + 3 * (10 / (12 / (3 + 1) - 1))
        22

        expr   : term ((PLUS | MINUS) term)*
        term   : factor ((MUL | DIV) factor)*
        factor : INTEGER | LPAREN expr RPAREN
        """
        result = self.term()

        while self.current_token.type in (PLUS, MINUS):
            token = self.current_token
            if token.type == PLUS:
                self.eat(PLUS)
                result += self.term()
            elif token.type == MINUS:
                self.eat(MINUS)
                result -= self.term()

        return result

def main():
    while True:
        try:
            # 在 Python3 下将 'raw_input' 替换为 'input'
            text = raw_input('calc> ')
        except EOFError:
            break
        if not text:
            continue
        lexer = Lexer(text)
        interpreter = Interpreter(lexer)
        result = interpreter.expr()
        print(result)


if __name__ == '__main__':
    main()

示例会话

将以上代码保存为 calc6.py文件，试一试，看看你的新解释器是否能正确解析含有不同运算符和括号的算术表达式。

以下是一个示例会话：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
$ python calc6.py
calc> 3
3
calc> 2 + 7 * 4
30
calc> 7 - 8 / 4
5
calc> 14 + 2 * 3 - 6 / 2
17
calc> 7 + 3 * (10 / (12 / (3 + 1) - 1))
22
calc> 7 + 3 * (10 / (12 / (3 + 1) - 1)) / (2 + 3) - 5 - 3 + (8)
10
calc> 7 + (((3 + 2)))
12

练习与总结

今天为你准备的新练习：

编写你自己的算术表达式解释器，如本文所述。记住：重复是学习之母。

恭喜你，你一直读到最后！你已经学会了如何创建（如果你完成了练习——你实际上已经编写了）一个基本的递归下降解析器/解释器，它能够解析复杂的算术表达式。

在下一篇文章中，我将更详细地讨论递归下降解析器。我还将介绍一种在解释器和编译器构建中非常重要且广泛使用的数据结构，我们将在整个系列中使用它。

敬请期待，下次见。在那之前，继续完善你的解释器，最重要的是：享受过程，尽情享受吧！

推荐书籍

以下是我推荐的几本书，它们将帮助你学习解释器和编译器：